Use (this Solvency II) case! Neuronale Netze treffen auf Least Squares Monte Carlo
Das Thema künstliche Intelligenz ist gerade in aller Munde und die Anwendungsgebiete erfreuen sich immer größerer Beliebtheit. In dieser Fallstudie wollen wir uns der Risikokapitalermittlung von Versicherungsunternehmen im Solvency II-Kontext widmen und wir werden den klassischen Least Squares Monte Carlo-Ansatz mit neuronalen Netzen herausfordern.
Die speziell für diesen Zweck erzeugten, realistischen Projektionsdaten von drei im Rahmen dieses Use Case aufbereiteten Lebensversicherungs- und Krankenversicherungsportfolien bilden den zentralen Bestandteil dieses Use Case.
Risikokapitalberechnung unter Solvency II
Solvency II zielt auf die Implementierung einer robusten Solvenzregelung für Versicherungen ab, die in angemessener Weise die tatsächlichen Risiken berücksichtigt. Eines der Kernkonzepte ist dabei die Berechnung der Solvenzkapitalanforderung (SCR). Gemäß Artikel 101 (3) der Richtlinie des europäischen Parlaments und des Rates „wird das SCR so kalibriert, dass gewährleistet wird, dass alle quantifizierbaren Risiken, denen ein Versicherungs- oder Rückversicherungsunternehmen ausgesetzt ist, berücksichtigt werden. Sie deckt sowohl die laufende Geschäftstätigkeit als auch die in den folgenden zwölf Monaten erwarteten neuen Geschäfte ab. In Bezug auf die laufende Geschäftstätigkeit deckt sie nur unerwartete Verluste ab. Sie entspricht dem Value-at-Risk der Basiseigenmittel eines Versicherungs- oder Rückversicherungsunternehmens zu einem Konfidenzniveau von 99,5 % über den Zeitraum eines Jahres.”
Demzufolge müssen die ökonomische Bilanz basierend auf einer marktkonsistenten Bewertung zum heutigen Zeitpunkt (Basisfall) sowie mittels einer geeigneten Approximationsmethode die erwarteten zukünftigen Cash-Flows zwischen dem Versicherungsunternehmen und den Versicherungsnehmern (versicherungstechnische Rückstellungen bzw. Technical Provisions) bzw. den Aktionären (Eigenmittel bzw. Own Funds) am Risikohorizont (1 Jahr) ermittelt werden. Um die in Solvency II vorgeschlagene Standardformel zur Berechnung des SCR zu umgehen, welche einen stark vereinfachten Ansatz darstellt und Schwächen bei den Annahmen aufweist, können Versicherungsunternehmen ein internes Modell zur SCR-Berechnung bei den Aufsichtsbehörden beantragen.
Funktionsweise eines internen Modells
Die typische Funktionsweise eines internen Modells ist in Abbildung 1 dargestellt. Die Generierung zahlreicher verschiedener Szenarien ermöglicht die Simulation einer empirischen Eigenmittelverteilung am Risikohorizont (1 Jahr gemäß Solvency II), welche die direkte Bestimmung des SCR (1:200 Perzentil gemäß Solvency II) ermöglicht. Dabei ist für jeden einzelnen Bewertungspunkt in t = 1 eine markkonsistente (und risikoneutrale) Bewertung der ökonomischen Bilanz erforderlich, welche durch Optionen, Asymmetrien und komplexe Abhängigkeiten getrieben ist. Der naheliegende Ansatz für jeden Simulationspunkt in t = 1 eine vollständige Monte Carlo Simulation durchzuführen, um u.a. mittels eines Cash- Flow-Projektionsmodells eine adäquate Bewertung durchzuführen, führt zu exponentiellen Rechenzeiten..
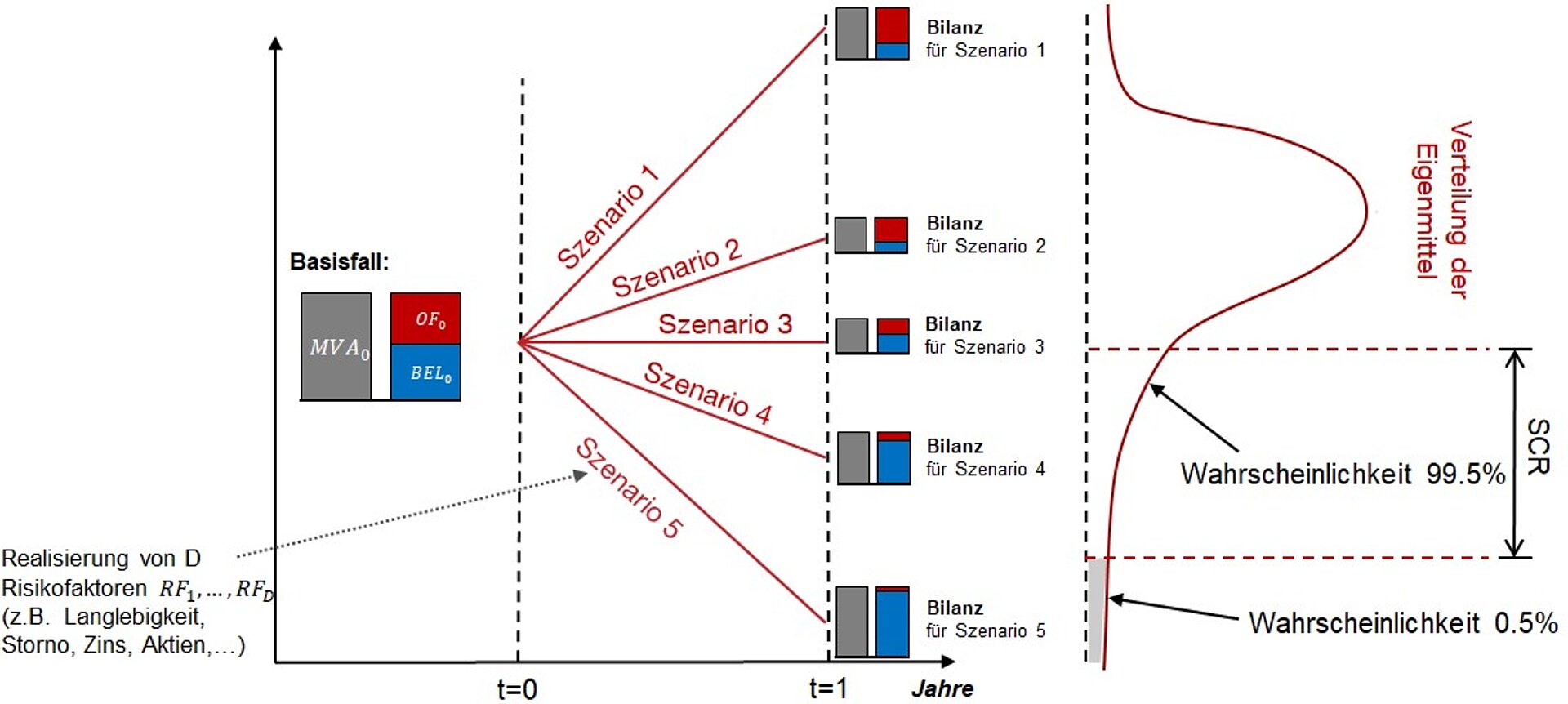
Abbildung 1: Bestimmung der Verteilung der Eigenmittel am Risikohorizont für verschiedene Szenarien: Ein Szenario besteht aus der Realisierung verschiedener Risikofaktoren wie Langlebigkeit, Zins, usw.; die Eigenmittel (OF) errechnen sich aus dem Marktwert der Assets (MVA) minus dem sogenannten „Best Estimate of Liabilities (BEL)".
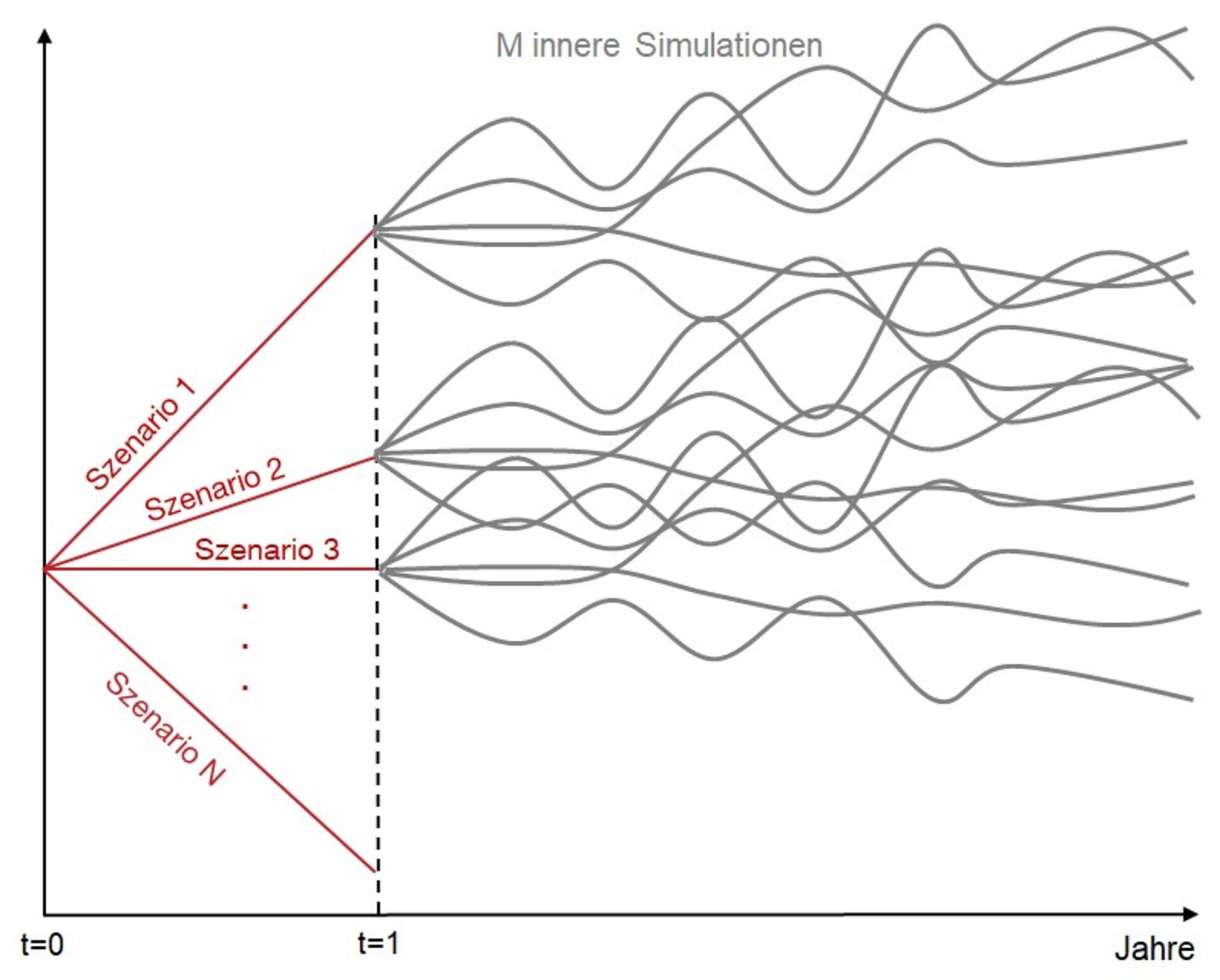
Abbildung 2: Generierung von M Simulationen in N Simulationen ("Nested Stochastics") zur Ermittlung der ökonomischen Bilanz in t = 1.
Regressionsbasierte Methoden zur SCR-Berechnung
Die moderne Antwort auf einen sogenannten "Nested Simulations"-Ansatz sind regressionsbasierte Methoden, welche einen allzu hohen Rechenaufwand und Speicherplatzbedarf vermeiden. Die Kernidee ist das Aufspannen eines geeigneten Fittingraums I1× ... ×ID, der durch die Intervalle Ik ∋ RFk für die zugehörigen D Risikofaktoren RF1,...,RFD definiert ist. Wie in Abbildung 3 dargestellt werden dann lediglich wenige innere Szenarien für jedes äußere Szenario (definiert durch den zuvor festgelegten Fittingraum) erzeugt. Der ungenaue Mittelwert von nur wenigen inneren Szenarien führt zu einem ungenauen, aber dennoch unverzerrten Fittingpunkt PV, welcher die Schätzung einer Bilanzposition (wie Eigenmittel oder BEL) in dem jeweiligen Szenario darstellt.
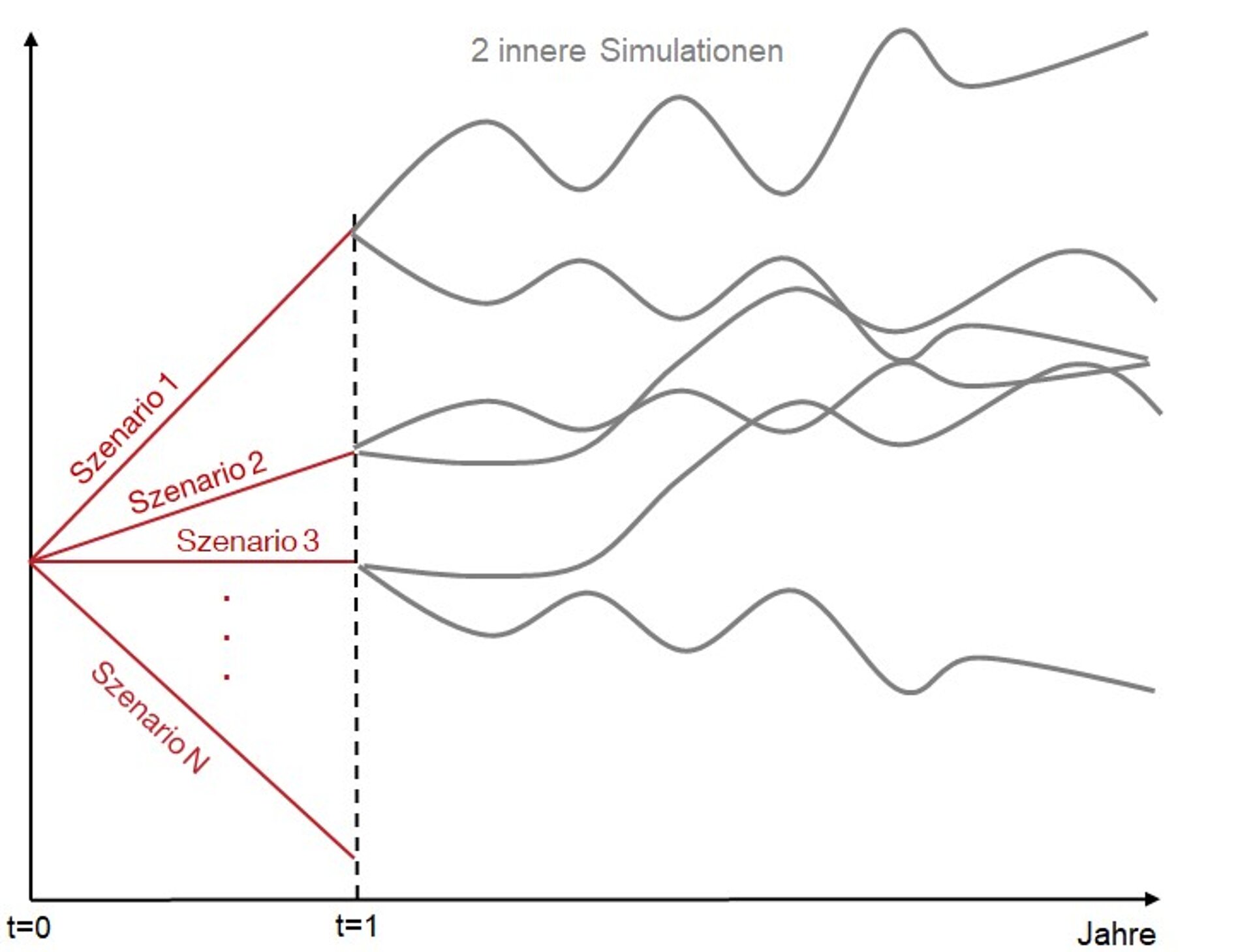
Abbildung 3: Generierung von wenigen inneren Simulationen (hier 2) für jedes Szenario zur Schätzung von Fittingpunkten (Bilanzpositionen).
Das Ergebnis ist eine Punktwolke mit verschiedenen Schätzwerten für die jeweilige Bilanzposition und es gilt einen funktionalen Zusammenhang herzuleiten. Eine praktikable Modellfunktion ist durch eine einfache Linearkombination von Basisfunktionen mit Koeffizienten am gegeben:
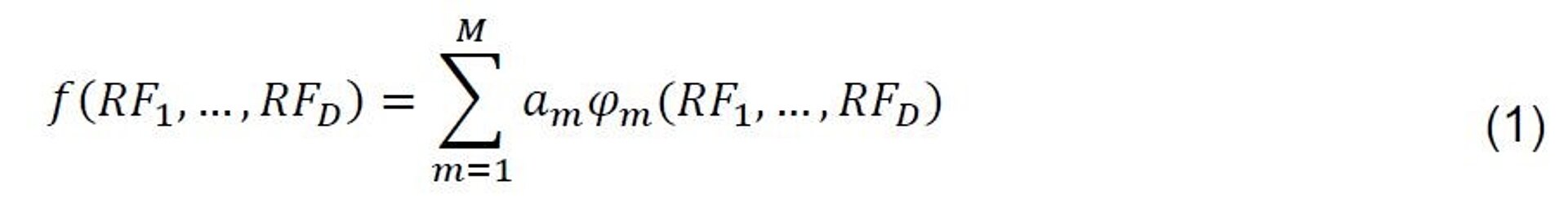
Als Basisfunktionen können beispielsweise Polynome oder radiale Basisfunktionen verwendet werden. Werden für n = 1,...,N mit PVn die Schätzwerte für Eigenmittel und mit RF1n,...,RFDn N simulierte Risikofaktorvektoren (äußere Szenarien) bezeichnet, kann die Funktion f mittels Least Squares bestimmt werden:
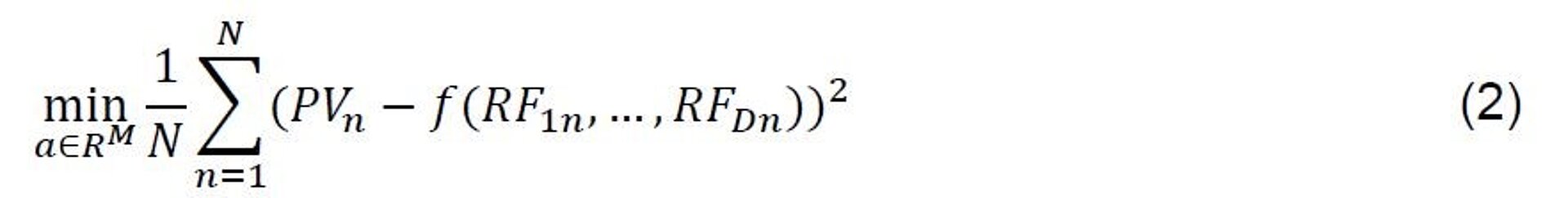
Abbildung 4 illustriert die Generierung einer Eigenmittelschätzung mittels einer Funktion mit Monomen als Basisfunktionen.
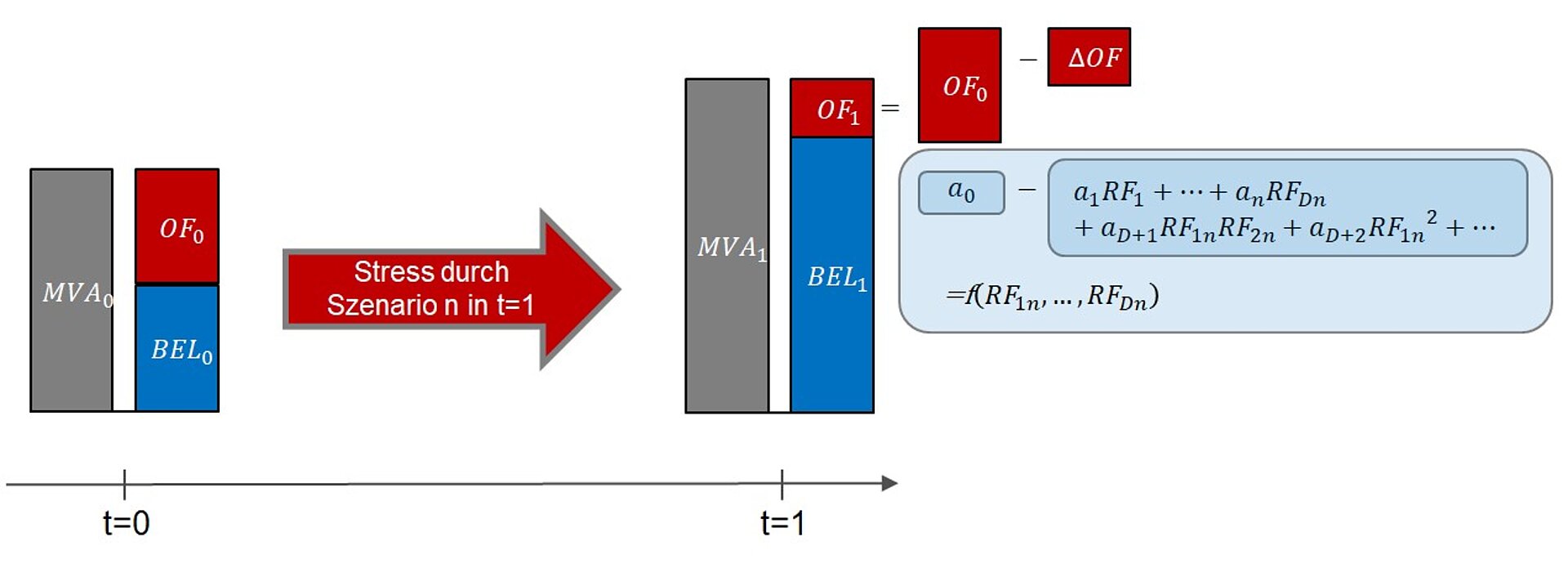
Abbildung 4: Erzeugung eines Schätzwertes für die Eigenmittel am Risikohorizont (t=1) für ein spezifisches Szenario n bei Verwendung von Monomen als Basisfunktionen: Die Konstante kann als Basis (t=0) und der restliche Teil der Polynomauswertung als Stress interpretiert werden.
Ein zweidimensionales Regressionsproblem ist in Abbildung 5 dargestellt.
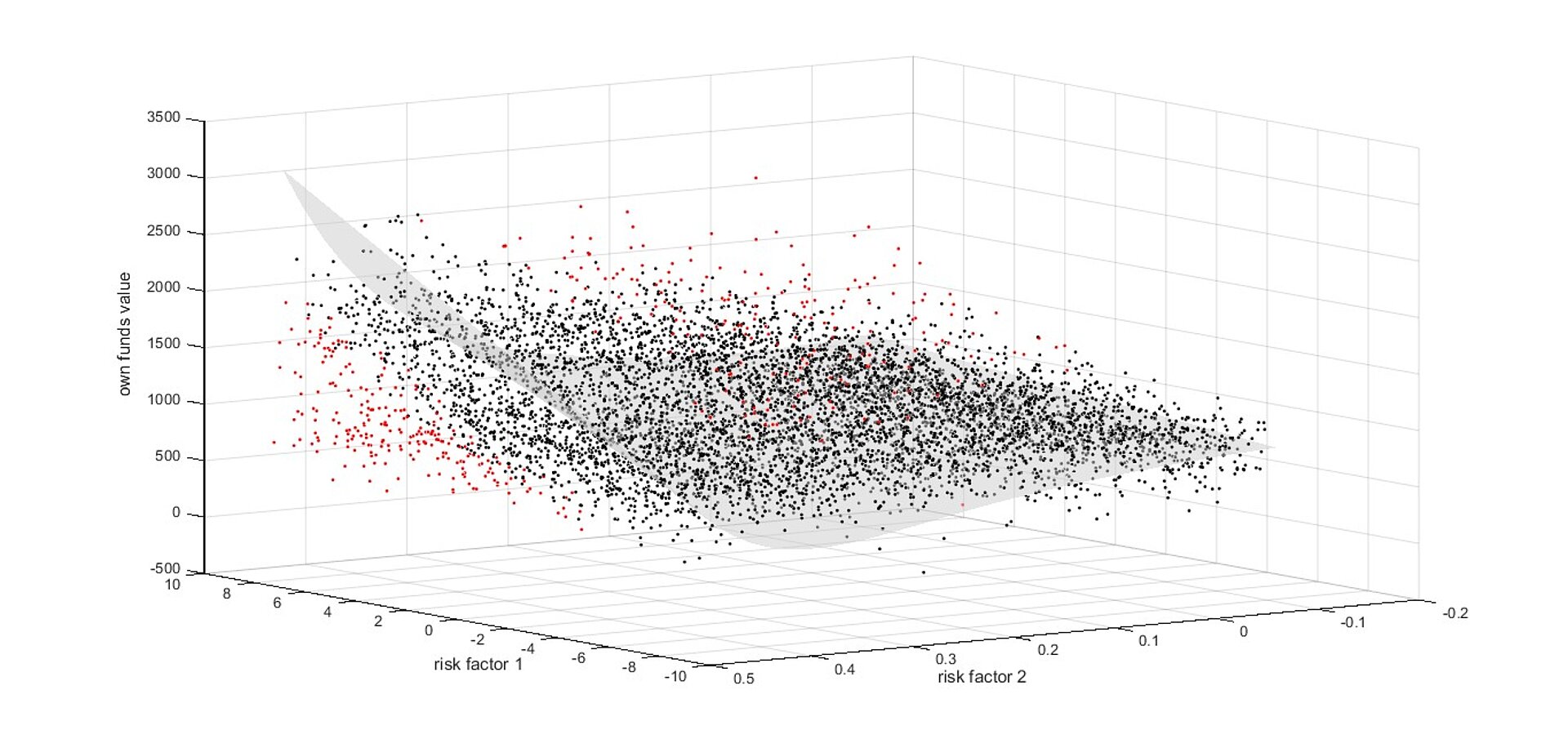
Abbildung 5: Eigenmittelfunktion für zwei Risikofaktoren, welche mittels Least Squares hergeleitet wurde.
Der Fokus dieser Fallstudie liegt auf der Verwendung von neuronalen Netzen für die Regression und es soll dabei der klassische Least Squares Ansatz herausgefordert werden. Dazu stellen wir einen umfangreichen Testdatensatz zur Verfügung, der eine adäquate Vergleichsanalyse zulässt.
Zugrundeliegender Datensatz
Das zur Verfügung gestellte Testdatenset orientiert sich an der oben ausgeführten Logik des klassischen Regressionsansatzes. Für das Training stellt das sogenannte Fitting-Datenset („train_input.csv“ und „train_result.csv“) ungenaue Auswertungen der Bilanzpositionen von einer Vielzahl von Risiko-Szenarien bereit. Mit Training bezeichnen wir die Herleitung einer geeigneten Funktion f. Wie in Abbildung 6 dargestellt erweist sich ein gleichmäßig ausgefüllter Raum als vorteilhaft.
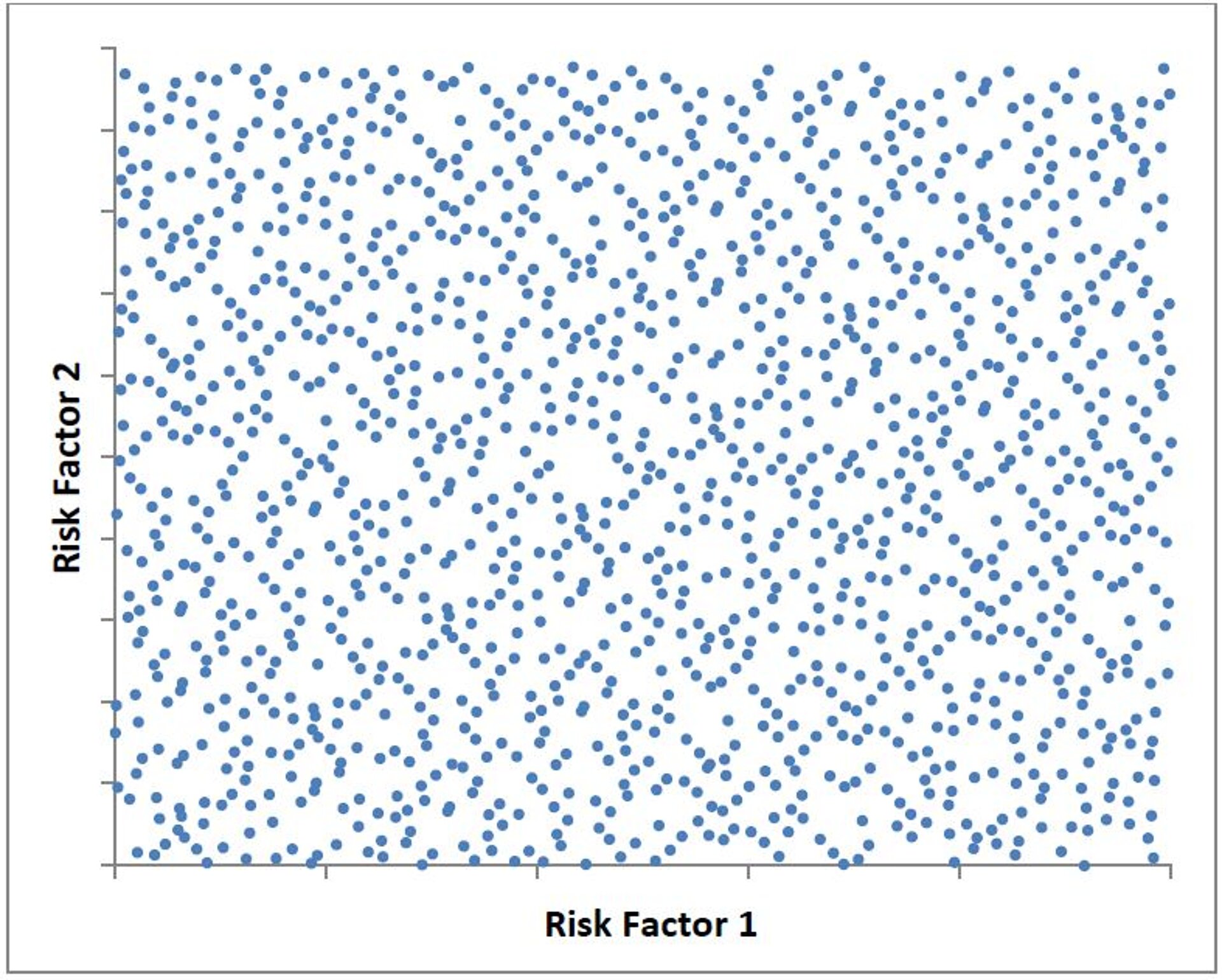
Abbildung 6: Fittingraum für zwei Risikofaktoren, welcher durch I1×I2 aufgespannt ist.
Konkret werden im vorliegenden Datensatz jeweils die Own Funds (Output) als Teil der gestressten Marktwertbilanz in den entsprechenden Szenarien dargestellt und entsprechen den Schätzwerten PVn, n= 1,..,215, von oben. Die Output-Werte basieren auf der Mittelung über lediglich zwei innere (riskoneutrale) Projektionen eines Cash-Flow-Projektionsmodells, welches einen beispielhaften aber dennoch realitätsnahen Versicherungsbestand von Leben- und Krankenversicherern abbildet. Das Projektionsmodell berücksichtigt dabei die Entwicklung von aktiv- und passivseitiger Bilanzpositionen und deren gegenseitige Interaktion über festgelegte Managementregeln. Die Szenarien werden durch Ausprägungen relevanter Risikotreiber RF1,...,RFD, D = 13 für die Portfolien 1 und 2, D = 12 für das Portfolio 3 (bspw. Zinslevel, Marktwertstresse, versicherungstechnische Stresse, etc.) repräsentiert.
Zur Überprüfung der Güte der gewählten Proxyfunktionen f kann das Out Of Sample Validation Set („validation_input.csv“ und „validation_result.csv“) bestehend aus 256 Szenarien herangezogen werden. Die dort dargestellten Werte basieren auf einer risikoneutralen Auswertung des oben beschriebenen Modells über eintausend Pfade. Somit stellen diese deutlich präzisere Schätzer der Bilanzposition, passend zum jeweiligen äußeren Szenario, dar, als im Falle der Fitting-Szenarien. Eine Proxyfunktion von hoher Qualität sollte in der Lage sein, die präzise simulierten Werte vorherzusagen. Zur Überprüfung der Güte eignen sich Statistiken wie etwa der durchschnittliche Absolutbetrag der relativen Abweichungen zwischen vorhergesagtem Wert (Proxy) und gemäß Monte Carlo berechnetem Wert (OOS Validation). Dabei ist zu beachten, dass die zu beobachtende Abweichung zum einen auf die Ungenauigkeit des gewählten Proxies zum anderen auf die Bewertungsungenauigkeit der Monte Carlo Simulation zurückzuführen ist. Um letztere besser einordnen zu können, enthält das Datenset für die OOS Validation zusätzlich für jedes Szenario den Standardfehler „stderror_validation.csv“ als Maß für die Ungenauigkeit des zugrundeliegenden Mittelwertschätzers.
Während die OOS Validation Punkte ebenfalls gleichmäßig im Risikotreiberraum verteilt sind, stellt das dritte Daten-Set, die SCR Region, ein alternatives OOS Validation Paket („nested_input.csv“ und „nested_result.csv“) dar, welches sich speziell auf einen gewissen Teilbereich des Risikotreiberraumes fokussiert (wiederum enthalten sind Outputvariable, Risikofaktoren und Standardfehler pro Szenario). Dabei stellt die SCR Region gerade eine Teilmenge der Risikoszenarien dar, deren Verluste in der Nähe des für das SCR relevanten 99.5% Quantil der Verlustverteilung liegen. Für die Portfolien 1 und 2 liegen 129 SCR Region Szenarien vor, für das Portfolio 3 sind es 50. Die Auswahl der Risikoszenarien hängt ansatzbedingt von den Ergebnissen einer vorher durchgeführten Regressions-/Proxy-Analyse ab, da erst mit Hilfe dieser die Gesamtverteilung der Bilanzpositionen und damit auch die relevante Verlustregion mit vertretbarem Aufwand bestimmt werden kann. Insofern stellt das Daten-Set zunächst also eine Validierung für einen anfänglich spezifisch gewählten Proxy-Ansatz dar. Unter der Voraussetzung, dass dieser ausreichend präzise ist, sollte sich die SCR Region aber auch bezogen auf andere Proxy-Ansätze als weitgehend stabil erweisen. Da die Auswertung der SCR Region im Sinne der Problemstellung essentiell ist, sind die Anforderungen an die Güte etwaiger Proxies besonders hoch. Um eine Verzerrung bei deren Beurteilung durch Monte-Carlo Fehler weitestgehend auszuschließen, wurden die Eigenmittel für Szenarien der SCR Region mit jeweils viertausend Simulationen ausgewertet und weisen daher nochmals einen deutlich niedrigeren Standardfehler als in den „normalen" OOS Validation Punkten auf, s. „stderror_nested.csv“.
Zur vereinfachten Interpretation der Ergebnisse wurden sowohl der Fittingraum I1× ... ×ID als auch die Output-Variable normiert, sodass die Eigenmittel im Basisfall für alle Beispielportfolien jeweils 1 ergeben. Mit Basisfall bezeichnen wir hier dasjenige Szenario, in dem alle Risikofaktoren,RF1×, ... ,RFD, den Wert 0 annehmen. Es findet, mit anderen Worten, keine Auslenkung der Risikofaktoren statt. Der für die Skalierung verwendete Referenzwert wurde auf Basis einer Monte Carlo Auswertung über 16.000 Pfaden bestimmt. Entsprechend der hohen Relevanz – das SCR stellt den 1-in-200-Jahren-Verlust dar, ausgehend vom Basiswert (s. Abbildung 1) – wurde somit die statistische Präzision der Basisauswertung gegenüber allen weiteren Szenarien (insbesondere gegenüber der des Basisszenarios als Teil des OOS Validation-Sets) nochmals erhöht.
