Neuronale Netze treffen auf Mortalitätsprognose
Abstract
Welchen Mehrwert können Neuronale Netze für die Prognose der Lebenserwartung in mehreren Populationen bieten? Zur Klärung dieser Frage wird zunächst eine Datenbasis mit Mortalitätsraten für Japan, USA, Deutschland und sechs weitere europäische Länder aufgebaut. In weiteren Schritten wird für jede dieser Populationen ein klassisches Mortalitätsmodell berechnet sowie das in Richman und Wüthrich (2018) vorgestellte tiefe künstliche neuronale Netz populationsübergreifend trainiert. Mittels dieser Modelle werden Mortalitätsprognosen für verschiedene Zeiträume erstellt und miteinander verglichen. Es zeigt sich bei der Mehrzahl der untersuchten Populationen eine bessere Prognosefähigkeit dieses populationsübergreifenden neuronalen Netzes im Vergleich zu einem „plain vanilla“ Lee-Carter Modell.
Obwohl unser Modell den Vorschlag zur Weiterentwicklung aus dem Kapitel 6 der Quelle Richman und Wüthrich (2018) durch den konsequenten Einsatz von Hyperparametertuning umsetzt, weisen die Ergebnisse nicht durchgehend die gewünschte Güte auf. Die vorwärtsgerichtete Architektur scheint die zeitliche Abhängigkeit nicht ausreichend gut erfassen zu können.
Die vorliegende Analyse ist als R-Notebook öffentlich zugänglich und kann von Interessierten einfach modifiziert und neu ausgeführt werden. Als Ergänzung zu Richman und Wüthrich (2018) wurde das Hyperparametertuning durchgeführt und die Vorhersage durch die Ensemble-Methode implementiert.
Unser Datensatz eignet sich zudem zum Training von diversen anderen Modellen. Insbesondere lassen sich damit neuronale Netze, welche sich besser für Zeitreihen-Approximationen als vorwärtsgerichtete Netze eignen, trainieren.
1. Datenbasis und Visualisierungen
Datengrundlage ist die Human Mortality Database (HMD, www.mortality.org), in der für 38 Länder u.a. die Bestands- und Todesfallzahlen differenziert nach Geschlecht, Alter, Jahr und Land verfügbar sind. Auf dieser Basis werden hier für die Länder Japan, USA, Spanien, Italien, Schweiz, Frankreich, Dänemark, Polen und Deutschland im Altersbereich 0 bis 100 Jahre die logarithmierten Mortalitätsraten (logmx) berechnet und für die vorliegende Untersuchung als Datensatz online bereitgestellt. Für Deutschland liegen die Zahlen getrennt nach „Ost“ und „West“ ab dem Jahr 1956 und für Gesamt ab 1990 vor. Aus den Basiszahlen wurde hier die Zeitreihe für Deutschland Gesamt zurück bis 1956 berechnet. Das gesamte hier betrachtete Zeitfenster geht vom Jahr 1956 bis zum Jahr 2016, wobei die Daten für Polen erst ab dem Jahr 1958 und für Italien nur bis zum Jahr 2014 verfügbar waren.
Der ursprüngliche Datensatz aus der HMD enthält einige Datenpunkte mit einer jährlichen Sterblichkeitsrate größer 1. Für solche Datenpunkte haben wir in unserer Datenaufbereitung die Sterberaten durch 1 ersetzt. An dieser Stelle sei angemerkt, dass in Richman und Wüthrich (2018) diese Datenpunkte unverändert verarbeitet werden, was eine Vergleichbarkeit zwischen den Ergebnissen in Richman und Wüthrich (2018) und in unserem Notebook schwieriger macht.
Auch ohne Modellierung ermöglichen die zugrunde liegenden Daten interessante Beobachtungen. Unten zeigen wir die Unterschiede in der Sterblichkeitsentwicklung zwischen Japan und den USA:
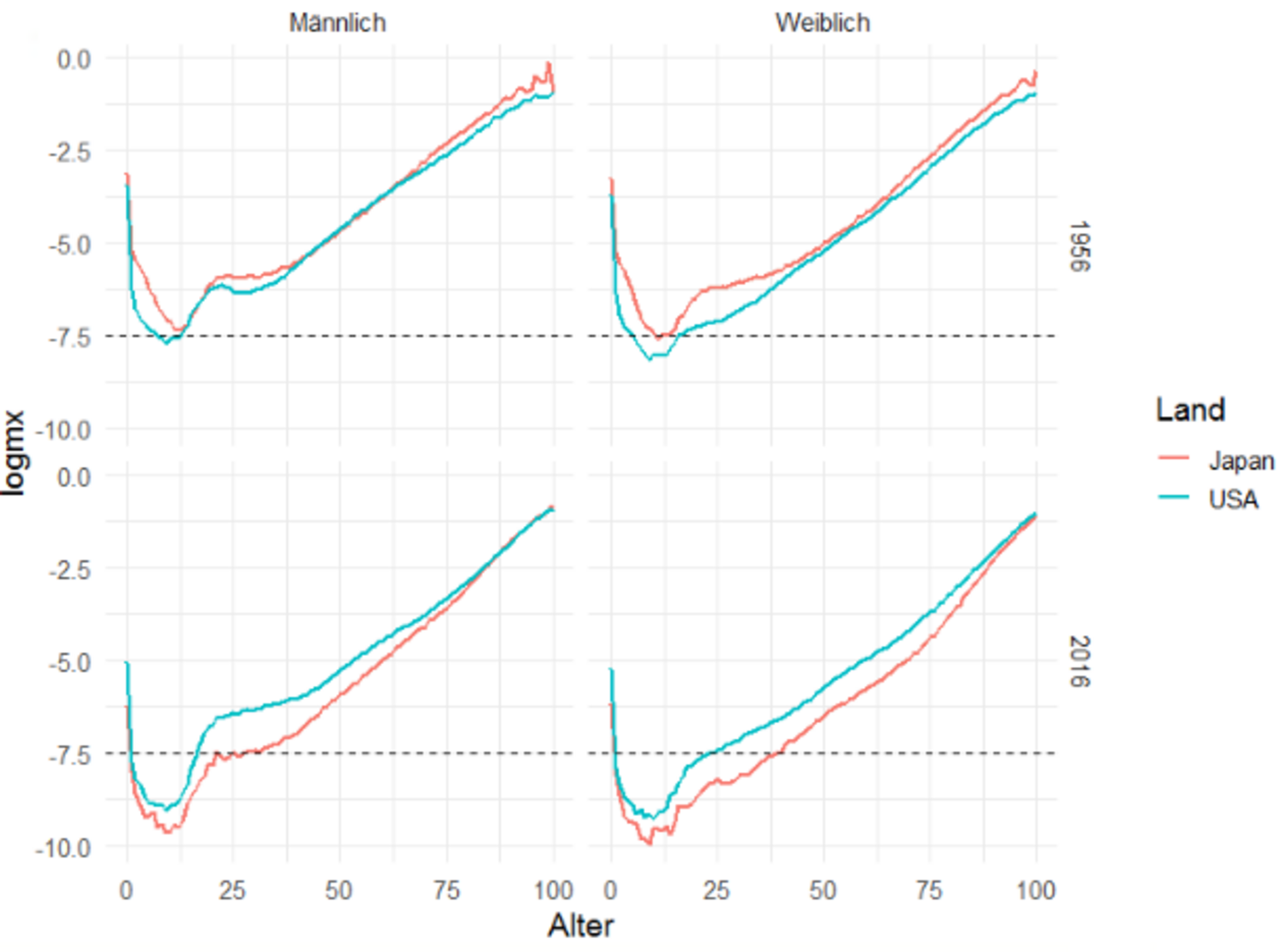
Demnach hat sich ganz offensichtlich zwischen 1956 und 2016 die Sterblichkeit in Japan günstiger als in den USA entwickelt.
Insgesamt umfasst die hier aufbereitete Datenbasis 143.218 Datenpunkte. Eine gute Möglichkeit, sich die Sterblichkeitsentwicklungen anzusehen und auch alle Datenpunkte zu Prüfzwecken zu visualisieren, sind die sogenannten „Heatmaps“ der logarithmierten Mortalitätsraten (logmx), hier am Beispiel Deutschland:
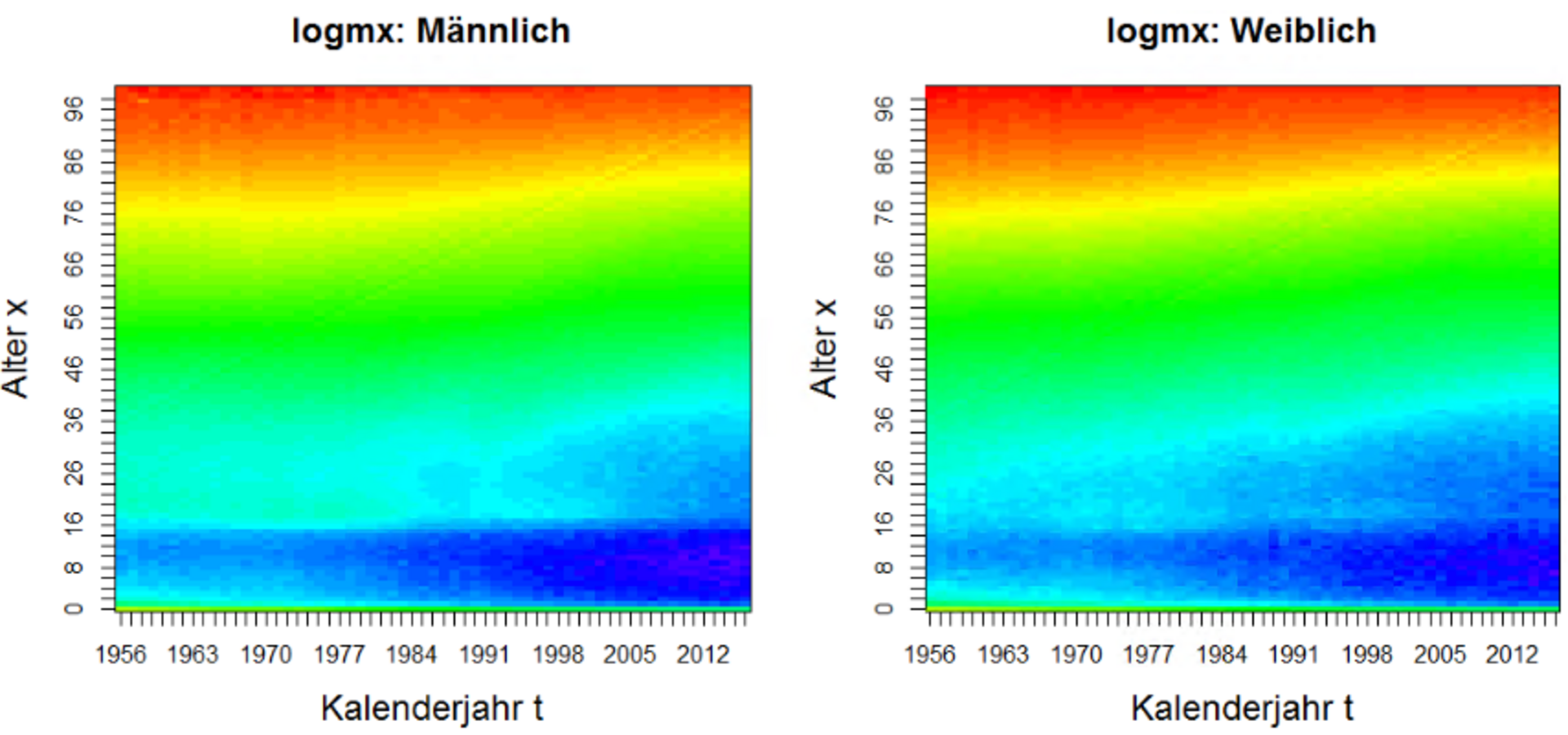
Als Farbpalette wurden dabei die Regenbogenfarben verwendet, von blau für sehr geringe bis rot für sehr hohe Sterblichkeitsraten. Mittels dieser Heatmaps können für Deutschland auch interessante Veränderungen der Lebenserwartung der Bevölkerung „Ost" im Vergleich zu „West" visualisiert werden (Differenz der logmx):
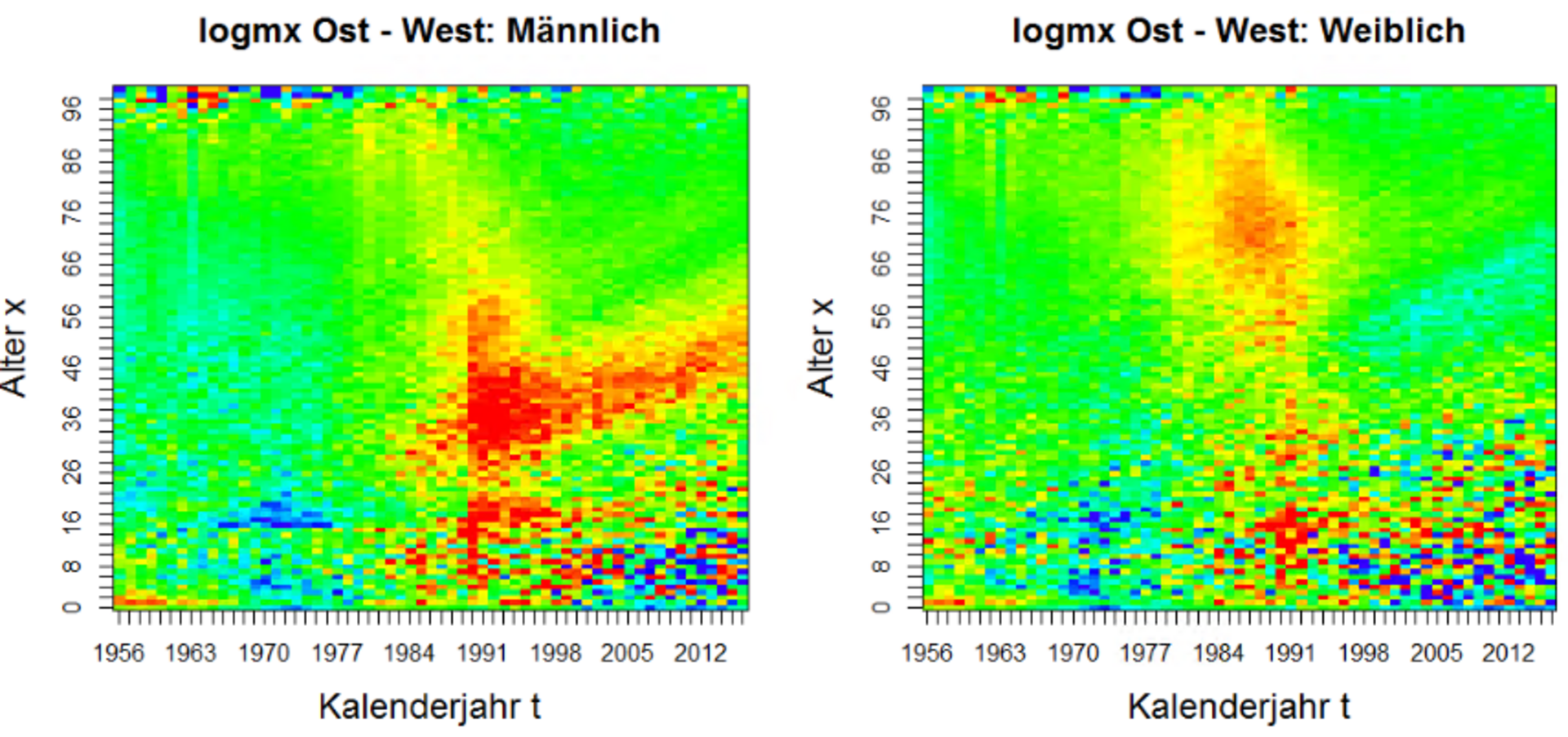
In den 1970er Jahren war danach die Sterberate von Kindern und Jugendlichen im Osten Deutschlands (DDR) teilweise geringer als im Westen. In den 1980er Jahren hat sich hingegen die Mortalitätsrate bei Ost-Rentnerinnen schlechter (gelb-rot) als im Westen entwickelt und ab 1990 liegt die Sterberate von Ost-Männern vor allem im Altersbereich 30 bis 50 Jahre teilweise deutlich über West-Niveau. Letzteres hält bis in die Gegenwart an und könnte sich auf die Prognoseergebnisse und -güte auswirken.
Als Anregung für die interessierten Leser*innen besteht die Möglichkeit, die getrennte Modellierung der Mortalitätsraten Deutschlands in Ost und West durchzuführen und zu prüfen, ob eine genauere Prognose dadurch möglich ist. Die auf „Kaggle“ (Link siehe unten) zur Verfügung gestellten Modelle werden mit Deutschland Gesamt gefittet.
Weitere Visualisierungen sowie die näheren Details zu den oben abgebildeten Graphiken können über das eingangs genannte R-Notebook eingesehen und bei Interesse ergänzt werden.
2. Modelle
a) Referenz „Lee-Carter"
Für die Modellierung der hinlänglich bekannten Jahrgangsabhängigkeit der Mortalitätsraten einer Kohorte gibt es zahlreiche Ansätze, von denen das 1992 von Lee und Carter vorgeschlagene Modell zu den einfachsten und bekanntesten zählt:
log(mx,t ) = ax + bxkt
wobei mx,t die Mortalitätsrate einer Person im Alter x im Kalenderjahr t, axdie durchschnittliche Mortalität im Alter x, bx die altersabhängige und kt die zeitabhängige Veränderungsrate bezeichnet. Für eine Mortalitätsprognose muss lediglich kt in die Zukunft fortentwickelt werden, siehe folgende Graphik für Deutschlands männliche Bevölkerung:
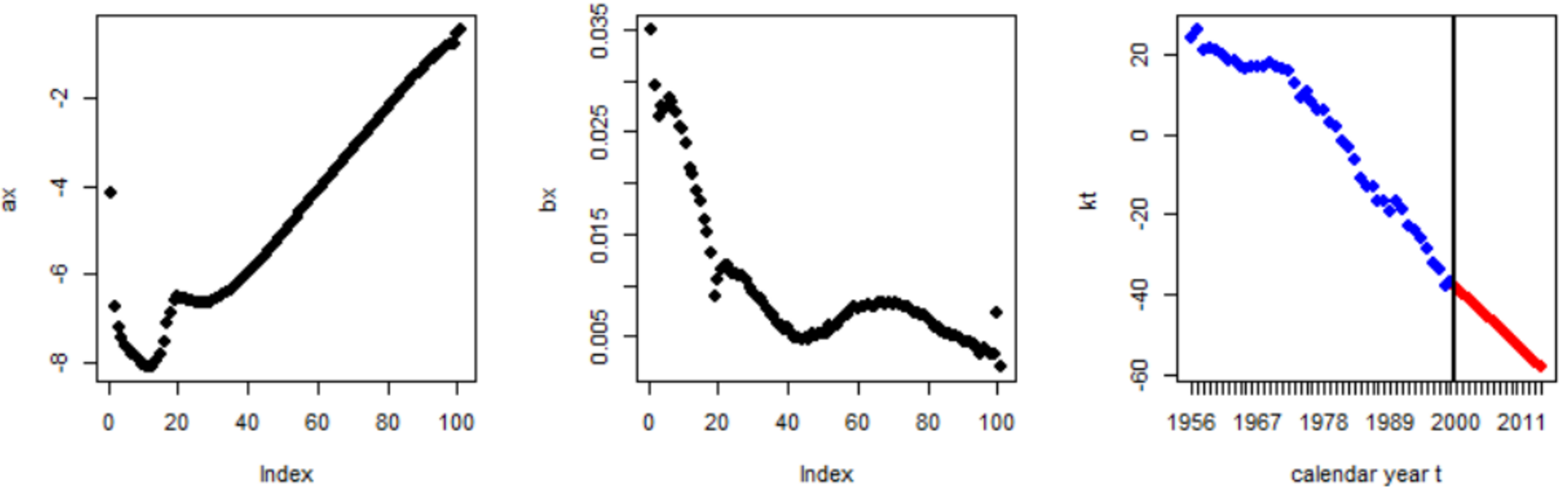
Die Modellparameter wurden hier durch eine Singulärwertzerlegung ermittelt und für die Fortentwicklung ab dem Jahr 2001 wurde die Zeitreihenmethode „random walk with drift" angewandt.
b) „Deep Learning" anwenden
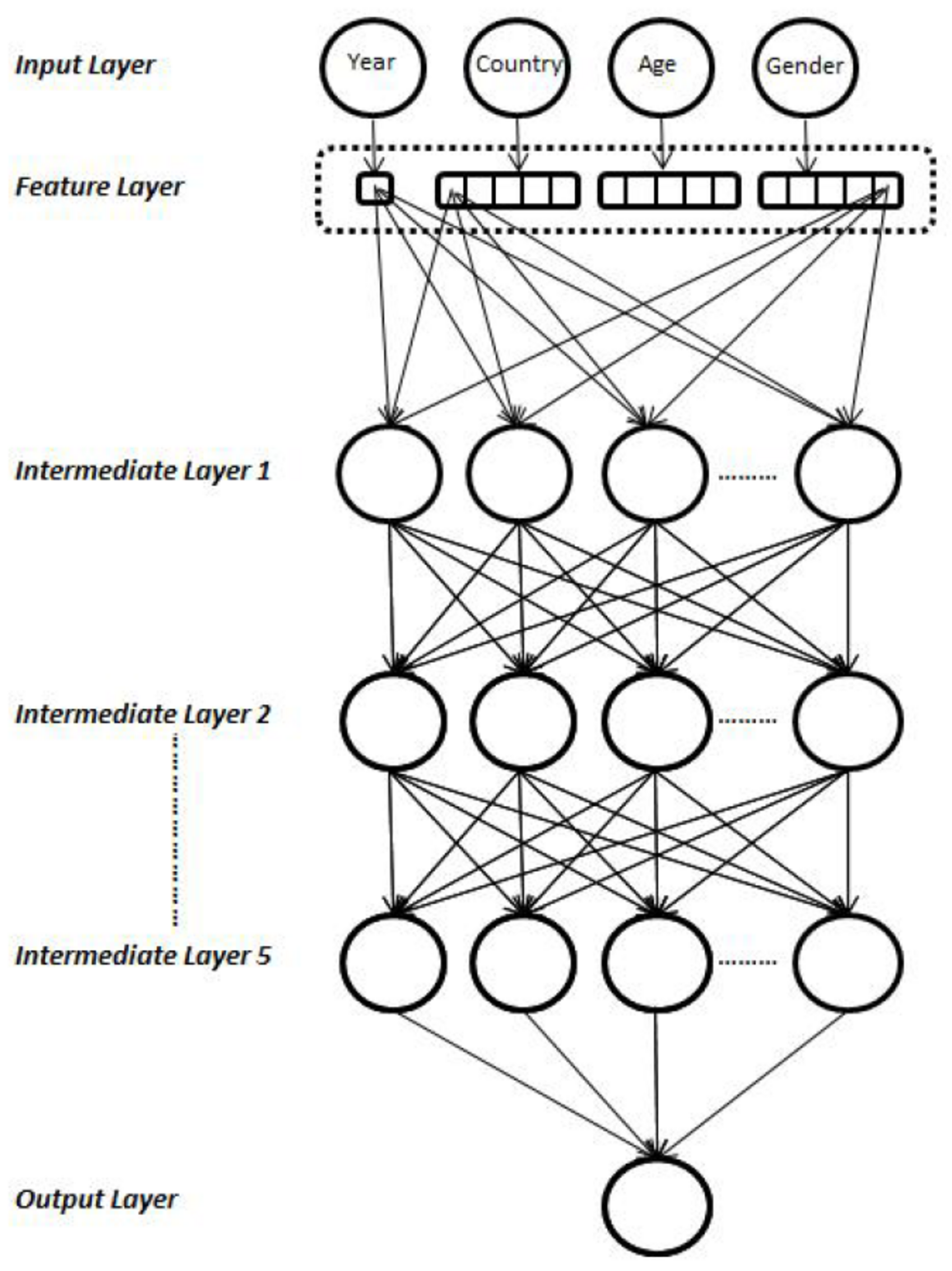
Im Fokus steht hier das in Richman und Wüthrich (2018) im Detail vorgestellte künstliche neuronale Netz mit fünf verborgenen Schichten. Bemerkenswert ist dabei auch die vorgeschaltete Dimensionsreduktion über eine eingebettete Feature-Layer bei den Eingabedaten sowie die Berücksichtigung einer „Skip-Connection". Das Netz in Richman und Wüthrich (2018) ist nicht nur tief, sondern mit je 128 Neuronen auch vergleichsweise breit und enthält über 70.000 zu berechnende Gewichte.
Für interessierte Leser*innen bietet das Notebook hier die Möglichkeit, auf einfache Weise die Dimensionierung der einheitlich 5-dimensionalen Embeddings für 'Country', 'Age' und 'Gender' zu verändern und die Auswirkungen auf die Prognose zu untersuchen.
3. Prognoseverfahren und Ergebnisse
Das Lee-Carter-Modell wird für alle 18 Land-Geschlecht-Kombinationen separat gefittet. Dabei werden analog zu den neuronalen Netzen die Daten von 1956 bis 2005 für das Training herangezogen. Die Kontrolle der Prognosegüte erfolgt mit den Daten von 2006 bis 2016.
Der Fehler des Lee-Carter-Modells auf diesen Testdaten von 2006 bis 2016 für alle Länder und Geschlechter beträgt 1.25×10-4. In Richman und Wüthrich (2018) wird für das mit unserem Ansatz vergleichbare Modell Lee-Carter (SVD) ein Fehler von 5.50×10-4 ausgewiesen. Hierzu ist es wichtig anzumerken, dass Richman und Wüthrich (2018) alle 38 Länder aus der HMD berücksichtigt werden. Die Sterblichkeitsraten für einige von ihnen lassen sich offensichtlich nicht so gut wie für die von uns ausgewählten neun Länder vorhersagen.
Neuronale Netze werden ebenfalls für die beiden Geschlechter mit den Daten des Zeitraums 1956 bis 2005 trainiert. Eine Prognose wird für den Zeitraum 2006 bis 2016 erstellt und bewertet. Für den Trainings-Zeitraum werden mittels eines automatisierten Verfahrens die Hyperparameter des neuronalen Netzes (z. B. Anzahl Neuronen und Dropout-Rate in den einzelnen Schichten) mit der besten Prognosegüte gesucht. Dabei werden insgesamt 108 verschiedene neuronale Netze trainiert.
Die zehn besten Architekturen der neuronalen Netze als Ergebnis des Hyperparametertuning sind in der folgenden Tabelle dargestellt. Der Mittelwert der Vorhersagen dieser neuronalen Netze definiert schließlich das Ensemble, welches wir mit dem Lee-Carter-Modell vergleichen.
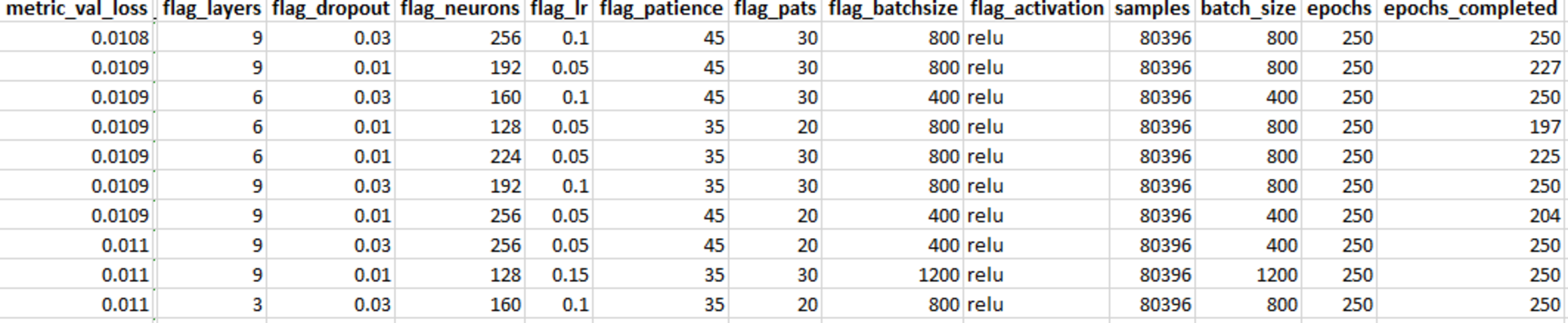
Der mittlere Fehler auf dem Test-Datensatz der Jahre 2006 bis 2016 für das Ensemble beläuft sich auf 0.92×10-4. Dies ist ein deutlich besseres Ergebnis als bei den Lee-Carter-Modellen. Trotzdem ist festzuhalten, dass lediglich bei 12 von 18 Land-Geschlecht-Kombinationen das Ensemble eine bessere Vorhersage als die Lee-Carter-Modelle liefert.
Unten wird zudem eine Zusammenfassung der Ergebnisse als Plots für alle Länder und Geschlechter aufgezeigt. Weitere Plots lassen sich leicht im Notebook umsetzen.
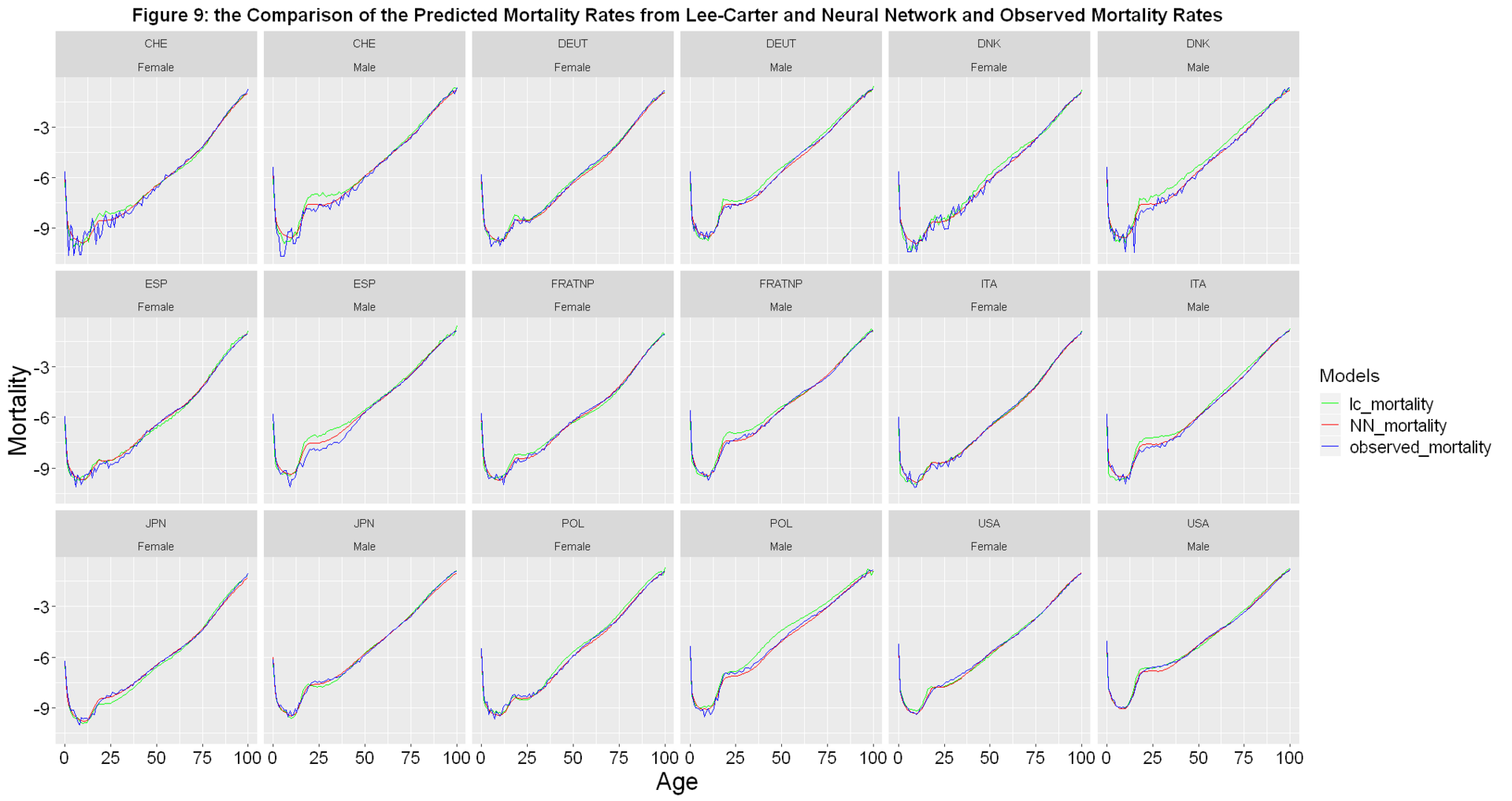
In unserem Notebook zeigen wir zudem die Vorhersage der neuronalen Netze in die weitere Zukunft. Dabei zeigt sich, dass manche neuronalen Netze, welche auf den Trainings- und Testdaten einen niedrigen Fehler aufweisen, offensichtlich unplausible Verläufe liefern. Dies bestätigt noch einmal die Unzulänglichkeit der vorwärtsgerichteten Architektur für die anspruchsvolle Aufgabe der Sterblichkeitsvorhersage.
4. Zusammenfassung und Ausblick
Am Beispiel des verwendeten Datensatzes konnte bei der Mehrheit der betrachteten Länder eine bessere Prognose des hier verwendeten populationsübergreifenden neuronalen Netzes im Vergleich zum Lee-Carter-Modell gezeigt werden. Trotzdem erscheinen die hier gewählten vorwärtsgerichteten Netze nicht in der Lage zu sein, verlässliche Vorhersagen der Sterblichkeit auch weiter in der Zukunft zu liefern.
Inzwischen gibt es weitere Veröffentlichungen zum gleichen Datensatz mit potentiell noch besseren Netzwerkarchitekturen. Für interessierte Leser*innen besteht hier die Möglichkeit, die in Perla et al. (2020) aufgelisteten R-Codes für rückgekoppelte Netze (LCLSTM) sowie für Faltungsnetze (LCCONV) ins Notebook zu integrieren.
Neben dem „plain vanilla" Lee-Carter-Modell gibt es allerdings noch einige weitere, komplexere Modelle in dieser Klasse der verallgemeinerten Alters-Zeit-Kohortenmodelle, für die i. d. R. ebenfalls höhere Prognosegenauigkeiten berichtet werden.
Die Arbeitsgruppe freut sich über Kommentare, Anregungen und abgeleitete Notebooks von Interessierten.
Quellen
Ronald Richman und Mario V. Wüthrich (2018), „A Neural Network Extension of the Lee-Carter Model to Multiple Populations", SSRN-Preprint 3270877
Francesca Perla, Ronald Richman, Salvatore Scognamiglio und Mario V. Wüthrich (2020), "Time-Series Forecasting of Mortality Rates using Deep Learning", SSRN-Preprint 3595426
